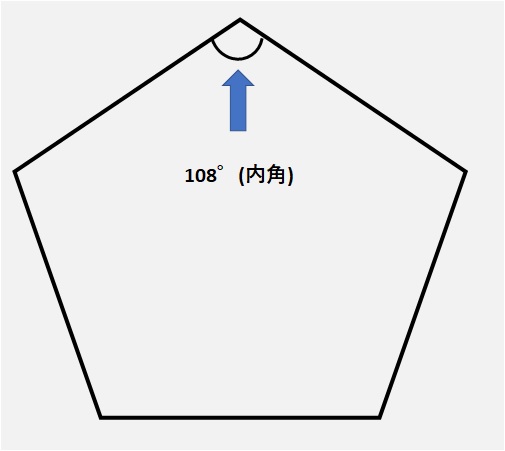
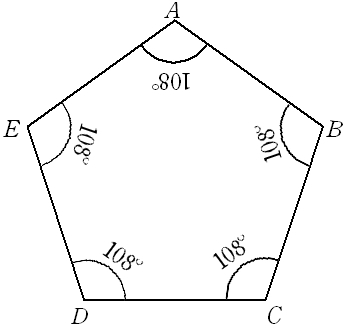
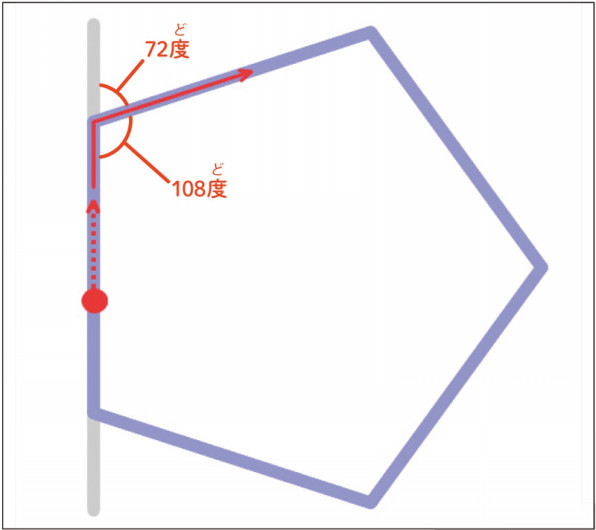
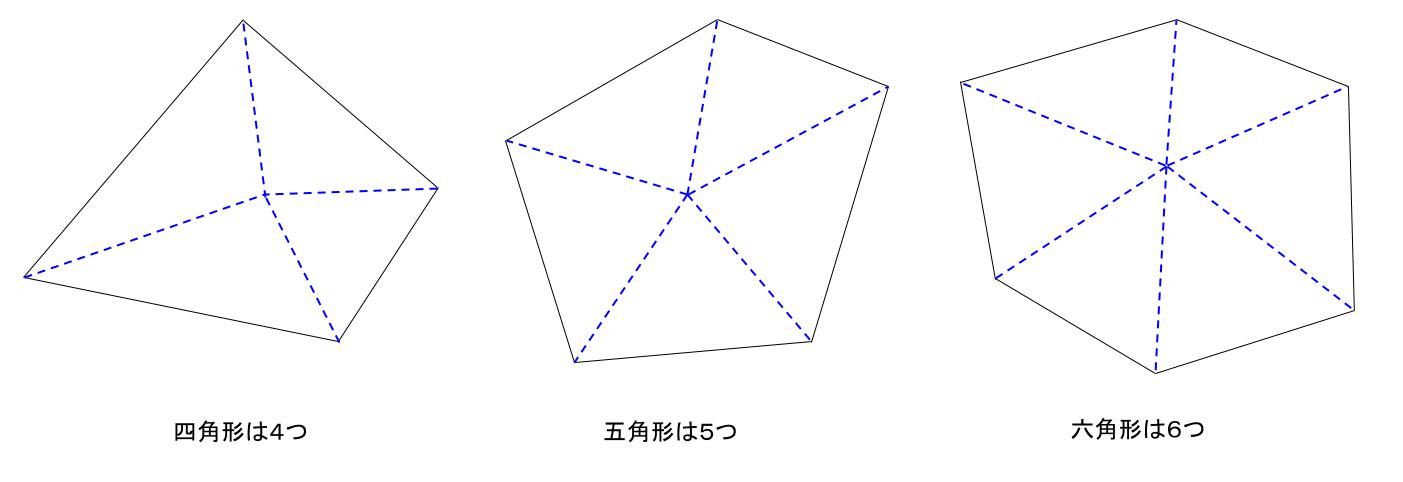
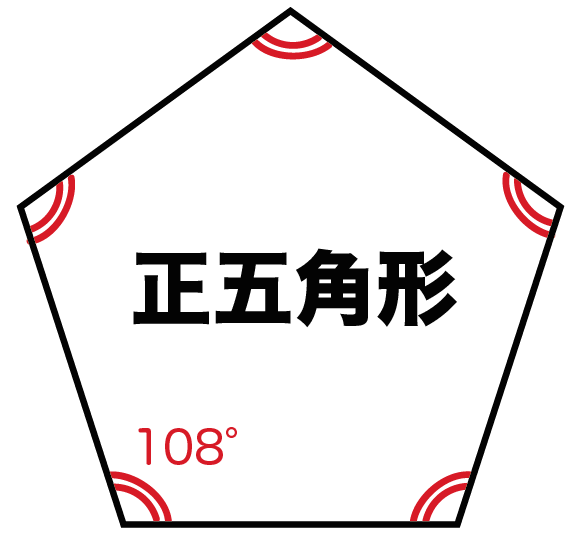
(五角形は,三角形3個分) 五角形の内角の和は,n=5を代入して, 180×(5-2)=180×3= 540°正五角形の一つの内角の大きさ )と一定な五角形である。辺の長さを a とすると 面 内角1つ分の大きさは \LARGE {=108° さっそく、正五角形の内角を計算してみよう! 星形の内角の和が180°になる理由 星形の角度が180°になる理由を説明していくために 三角形の外角の性質を知っておく必要があります。 このように 三角形の外角は、隣にない内角2つ分を合わせた大きさになるという性質があります。 これを利用して
プログラミングで正多角形を書く6つのステップ プログラミング教育 小学5年算数
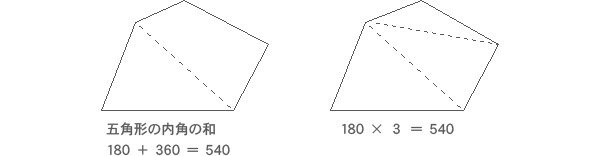
五角形の内角の和
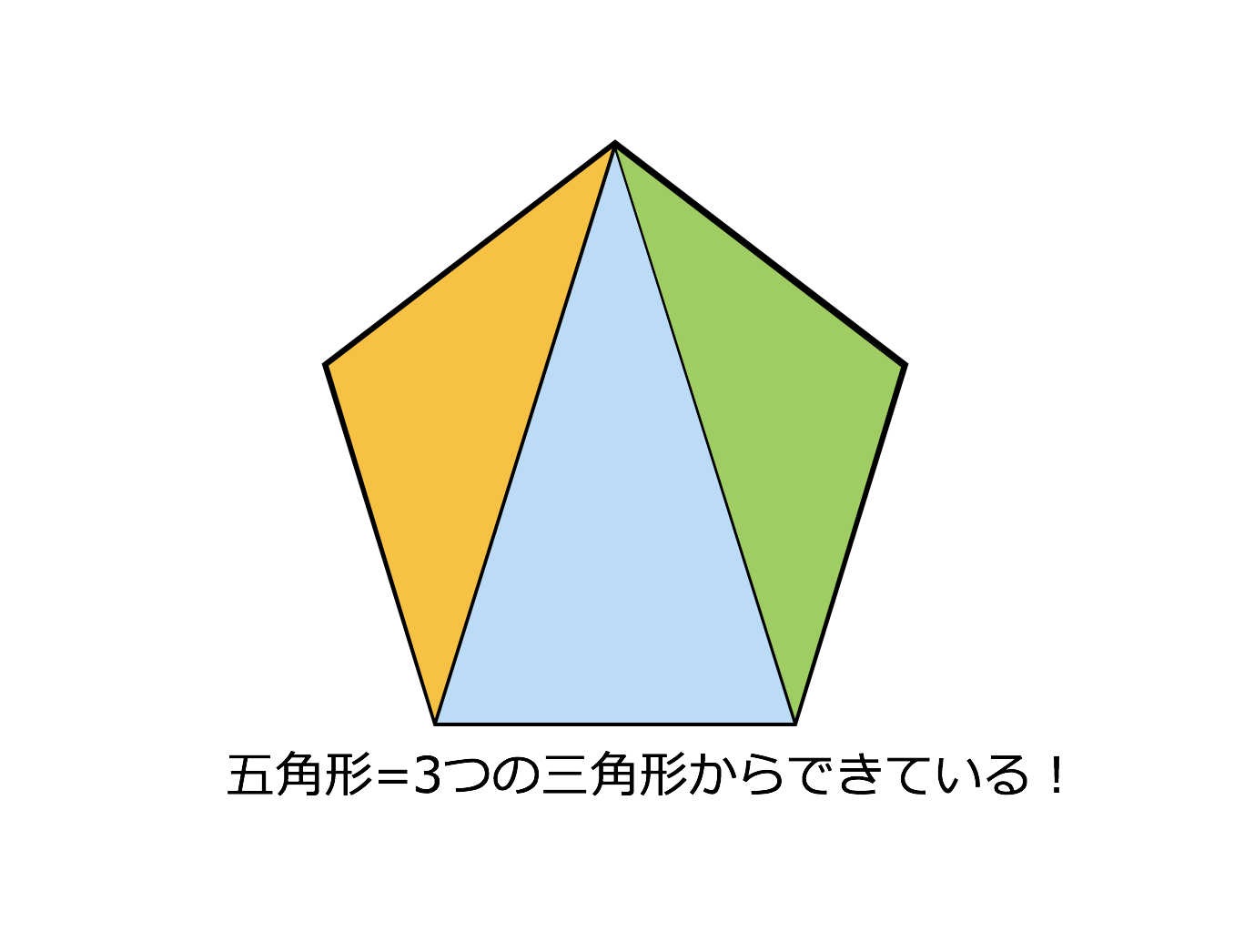
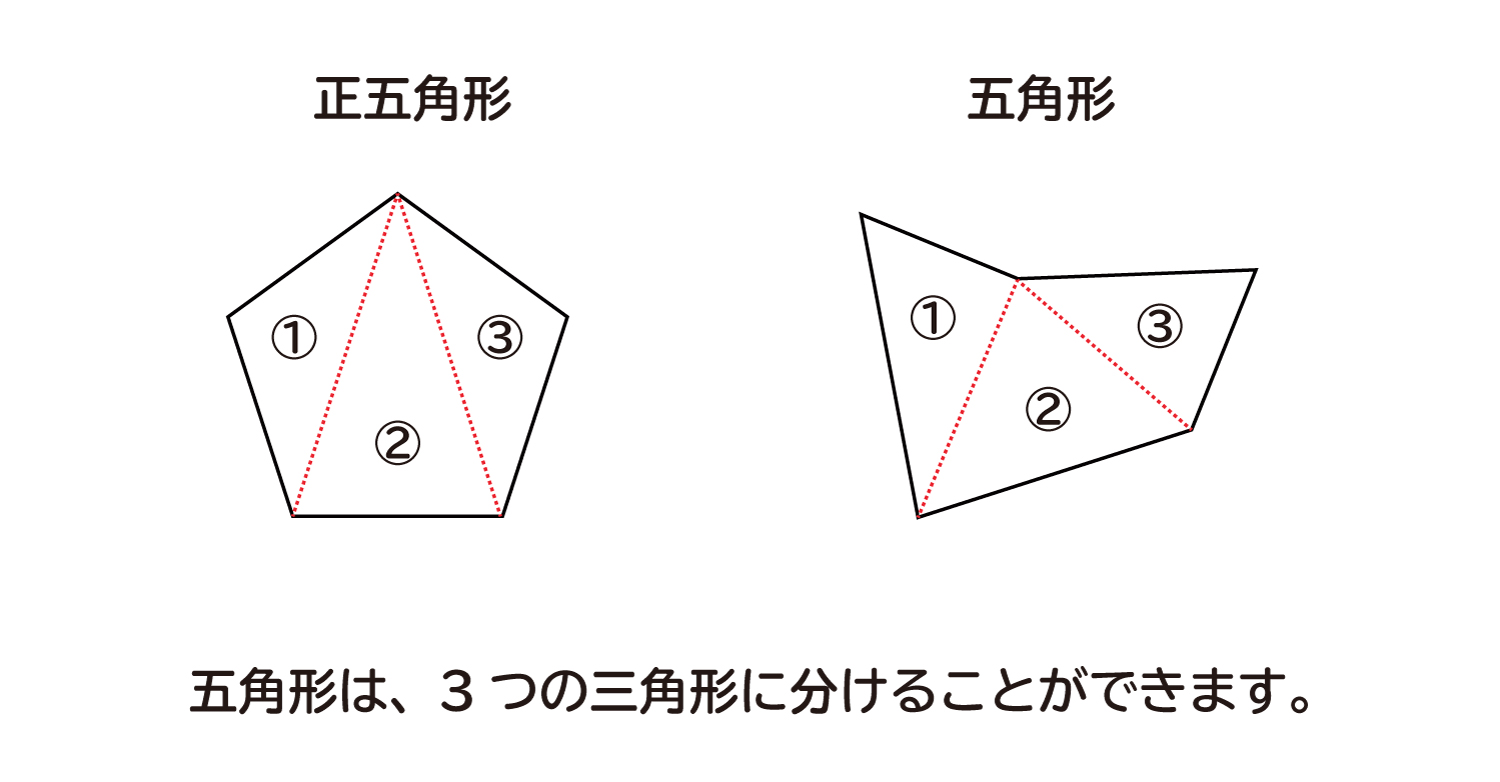
五角形の内角の和- 正五角形の内角は108° するとここを頂角にした二等辺三角形が見えてきたと思うので、底角を出す。さっそく二等辺三角形が出てきてうれしい。 ここの角度が36°と求まる 正方形の内角は90°なので、下の赤い角は180-(36+90)=54(°)。 ここは54° 正方形と同じように、頂点dから対角線を2本引きます。すると三角形が3つあることが分かります。なので、正五角形は「 三角形の内角「180度」×3個分 = 540度 」になります。また、正五角形は、同じ角度の角が5つなので、「 540度 ÷ 5つ = 108度 」です



正五角形を描く ウソの国ー詩と宗教 戸田聡 St5402jp
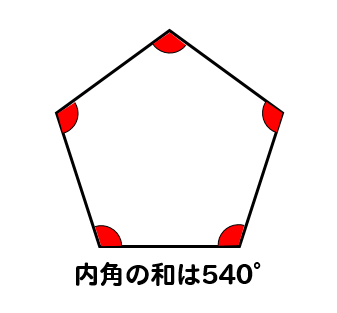
後悔(五角形の内角の和) 三角形や四角形の内角の和をまとめ,多角形の内角について考えていきます。 「180とか360とか中途半端だよねえ。 どうせなら100や0なら覚えやすいのにね。 」 とふってみました。 しかし何の反応もありません。 仕方なくS:四角形,五角形の内角の和は,360度,540度になりそう。 学習課題(5時間目) 四角形,五角形の内角の和を調べていくことでどのようなことがわかるだろうか。 多角形の角 となることがわかる。 次時に繋げる「Whatifnot」・ 「五角形」「六角形」「多角形」の・探究的な活動 ことを理解している。 4 定義を知る。 ・説明する活動 / ・ 五角形,六角形の内角の和を,三 8 角形に分割して調べ,多角形の内角 の和について表にまとめる。 ・ 多角形の内角の和のきまりを考え る。
五角形の内角の和は「三角形の内角の和(180°)」を3倍した 180°×3 = 540°(2)主眼 星形五角形の内角の和を既習事項を使って、求めることができる。 (3)展開 学 習 活 動 指 導 および 支 援 時間 備考・ICT機器 評価(方法) 1.星形五角形の内角の 和が何度になるか、 予想し,調べる。 (本時のめあて) 2.自分の考えで問題に挑戦してみよう! 正多角形の内角・外角 まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる!
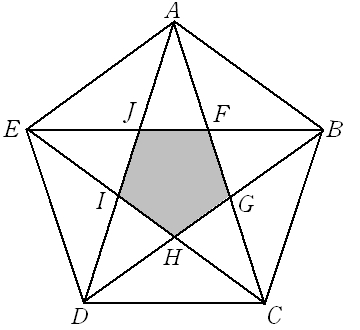
・五角形の場合:n=5 ・内部に作成できる三角形の数:n-2=5-2=3個 540度 どうですか?五角形の内角の和は540度で間違いないですよね? したがって、 となるのです。これが 公式 ですよ^^また,星形五角形や星形七角形は一筆書きでかけますが,星形六角形や星形 八角形のときには一筆でかけない場合があります。星形が一筆書きでかける のはどんな条件のときか,調べてみましょう。 星形多角形の内角とは,多角形多角形の外角の和凹型四角形の角星形五角形の内角の和 本時のねらい 「多角形の外角の和の求め方を導き、それを利用することができる。」 「これまでの既習事項を用いて凹型四角形の角や星形五角形の内角の和の求め方を説明することができる。



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
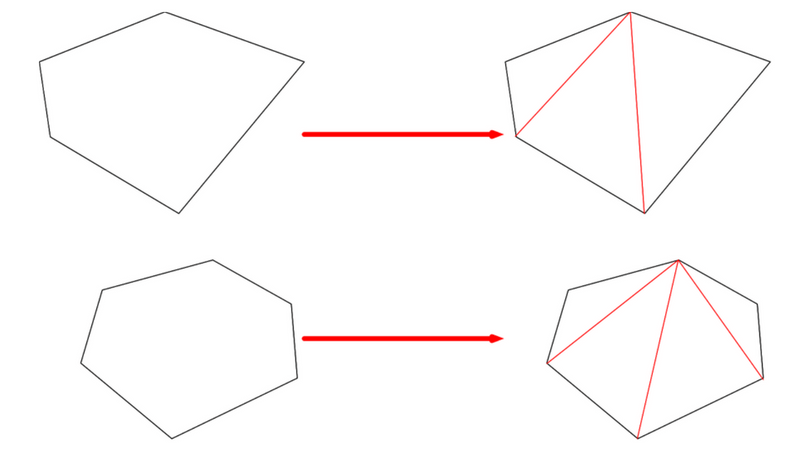
三角形の数は(52=3)で求めることができます。 三角形の内角の和は180°なので、五角形の内角の和は、180°×3=540° になります。 多角形の角の性質を下の表にまとめました。必ず覚えてください。この表を理解することで、どんな多角形が来ても内角の和を中学数学五角形、内角ver 100produced by dadaadaaahttps//twittercom/dadaadaaaRECREAA All Rights Reservedhttp//recreaacom/「五角形や六角形の内角の和を求 める方法を考えよう」 <五角形> ⇒三角形が3つできるから <六角形> 生徒は板書,あるいはノートに記入しながら発表する。 ⅰ.対角線が1本しか引けない。 対角線が引けていない四角形に目を向け させる。
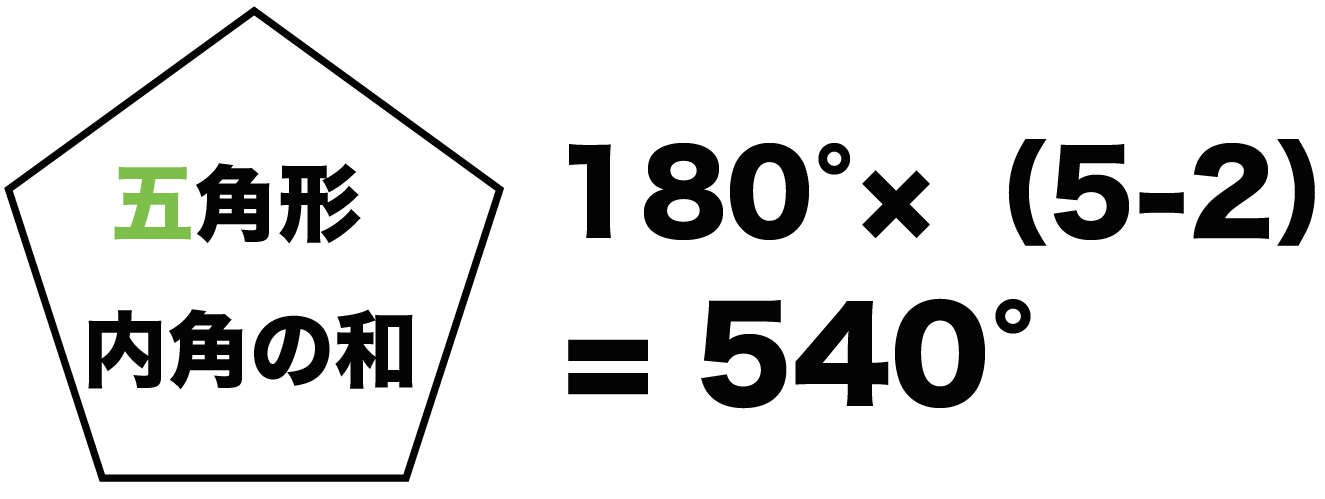



簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく



直角正五角形
正十五角形 正十五角形においては、中心角と外角は24 °で、内角は156°となる。 一辺の長さが a の正十五角形の面積Sは = = ( ) (/) は有理数と平方根の組み合わせのみで表せる = = ( ) 正十五角形の作図 正十五角形は古代から定規とコンパスによる作図が可能であることが知られていた図形課題学習の指導(数学) 1. 教材 「星形多角形の内角の和を追究しよう」(2年) 2. 教材観 三角形や多角形の内角の和を学習した後で,発展問題としてよく扱われる教材である。 星形五角形だけとっても,その形のきれいさで生徒の興味・関心を五角形の内角の和 整理番号から検索 ©19 学校図書株式会社 > もくじトップ < > 推奨環境 < > 使い方の注意



茗渓予備校 科目別データベース




小学5年生 正多角形 算数 Active Learning 学院
「五角形」、「六角形」や「多角形」 の用語とその定義を理解し、それぞ れの形の内角の和を求めることが できる。 ・ 五角形の内角の和を工夫して求 め、540°であることを説明する。 ・ 多角形の内角の和を表にまとめ る。 児童が説明する算数的活動(3) 正五角形では5つの外角の和は ゜だから1つの外角は ゜ したがって1つの内角は ゜です. 何角形でも外角の和は360° この問題は五角形の内角の和が540°になることを使っても求められるが,初めの2つの空欄を埋めるには,問題文で指定された順に答える方がよい.四角形、五角形、六角形・・・十角形なんかもそうだね。 三角形の内角の和 (角度を全部たしたもの)が 180° になるのは知っているよね。 では、角が多い、多角形の内角の和はどうなるんだろう。




スタディピア 平面図の内角の和




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく
・五角形、六角形の内角の和を求める。 ・ 多角形の内角の和について表にまとめ、きまりを考える。 (探究的な活動) (説明する活動) 三角形の内角の和を基に、多角形の内角の和を三角形に分けて求める方法を考え、説明している。数学的な考え方内角の和は 180°×2=360° となった。 五角形の場合も同じように考えると、 3 つの三角形がで きるので、内角の和は 180°×3=540° 六角形の内角の和は、 180°×4=7° n 角形の場合を考えると、一つの頂点から対角線を引い 正五角形は頂点が5つあるから、 さっきの公式のnに「5」をいれるだけでいいんだ。 すると、 180 × (n2)/n = 180×(52)/5 = 108° になるね。 つまり、 正五角形の内角の大きさは「108°」ってことさ。 くそ便利でしょ??^_^ なぜ正多角形の内角が計算できるの



図形 正五角形の分解 父ちゃんが教えたるっ




多角形の内角の和 外角の和の公式 数学fun
四角形の内角の和: 360° 360 ° 五角形の内角の和: 540° 540 ° 六角形の内角の和: 7° 7 °2年 多角形の外角|数学イメージ動画集|大日本図書 五角形の外角を全部合わせると 360° です。 同様に,他の多角形でも外角の和は 360° になります。 このことから,多角形の外角の和はいつも 360° になるということがわかります。 実施時期 2年生2五角形の場合はそれが5つあるので、五角形の外角と内角の和が900°であることが分かっています。 一方で、内角の和は先ほど求めたように、 180°×3=540° ですね。




中学数学 三角形と角 五角形の内角 Youtube




小5 算数 小5 33 五角形 六角形 多角形 Youtube
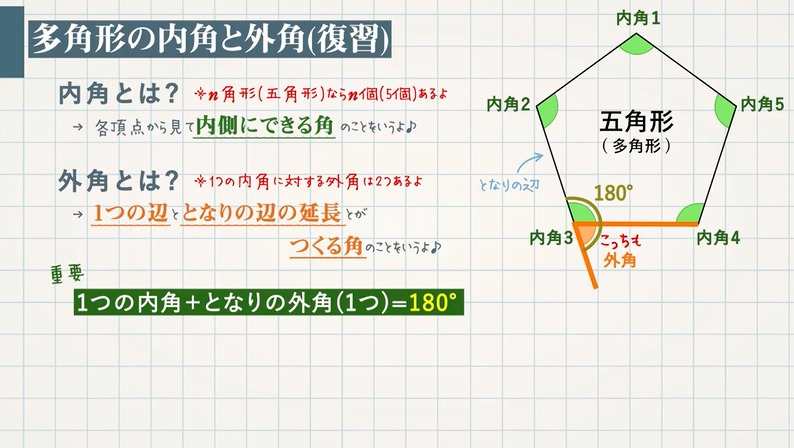
三角形の内角と外角 $ ABC$ において,$\angle A,\angle B,\angle C$ を,$ ABC$ の内角といいます. また,下図の $\angle ACD$ や $\angle BCE$ のように,一つの辺とその隣の辺の延長がつくる角を,外角といいます. さて,三角形の内角と外角について,次の重要な事実が成り立ちます. 正五角形がイラスト付きでわかる! 全ての辺と角が等しい五角形。 概要 正多角形の一種であり、全ての辺の長さと角の大きさが同じな五角形である。 五角形の内角の和は540度なので、正五角形の内角は全て108度となる。 全ての対角線を結ぶと、五芒星(ペンタグラム)に、輪郭を取り出右の表のように,n角形を三角形に分けると, 内角の和は 180°×(n−2) になる. ≪例≫ 三角形の内角の和は180° 四角形の外角の和も360° 五角形の外角の和も540°



五角形の内角の和 Geogebra



スクラッチ入門 16 正五角形をかいてみよう はじめる 楽しむ プログラミング こどもプログラミング教育のツボ ジャムハウス
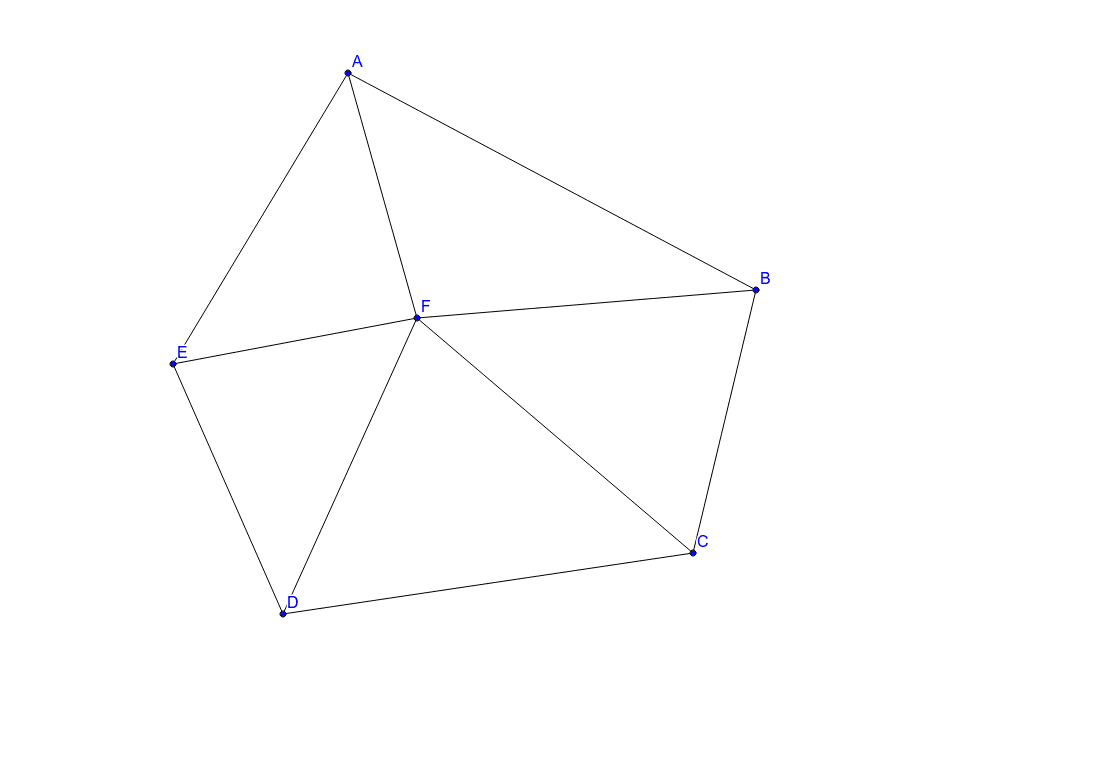
2-4-1 星型多角形の内角の和 教材(問題場面) 図のように5つの点A,B,C,D, Eがある。



1



三角形の内角と外角の性質 教遊者



茗渓予備校 科目別データベース




無料 中2数学 標準問題 解答プリント 223 図形3 多角形の角



中学数学 多角形の内角 外角 中学数学の無料オンライン学習サイトchu Su




正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より



三角形の内角の和が180度である理由と外角の和や多角形の公式 まぜこぜ情報局




多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト
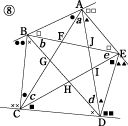



課題学習の指導 数学



正五角形の内角 外角



正五角形の作図法 数理女子



Q Tbn And9gctqxnxegjdxp Adpruavnpmf2sansioyhqkmwlqdbcw Fiiw67x Usqp Cau



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス




多角形の外角の和 凹型四角形の角 星形五角形の内角の和 Ppt Download




五角形 Wikipedia




プログラミングで正多角形を書く6つのステップ プログラミング教育 小学5年算数



1



重なる形と図形の角を調べよう 第5学年 小学校 算数 My実践事例 日本文教出版




正多角形の内角と外角の大きさ 具体例で学ぶ数学



多角形の内角の和 は何度なのか を説明します おかわりドリル




8 Times31 Descubre Como Resolverlo En Qanda



Math 多角形の内角の和 働きアリ



多角形の内角の和の公式と外角の和を利用した角度の求め方
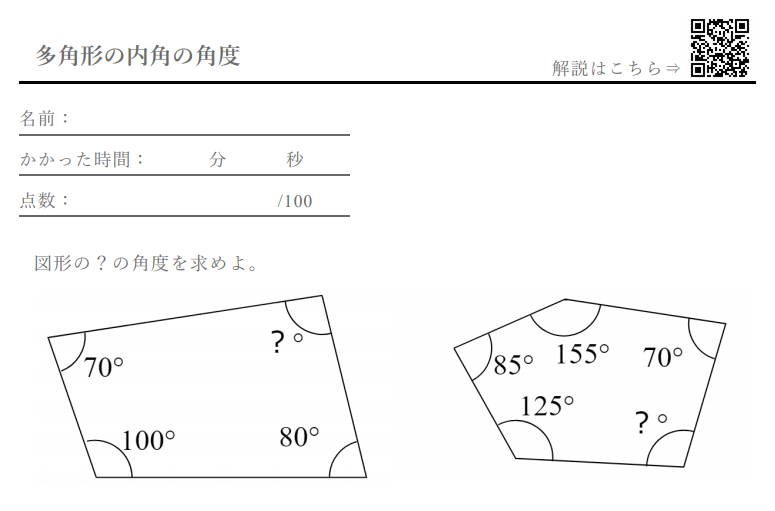



多角形 の内角の角度 計算ドリル 問題集 数学fun




内角の和 算数用語集



正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




8 Times31 Descubre Como Resolverlo En Qanda



中二 五角形の内角の和の求め方 をアップ 久保塾 今治市の学習塾




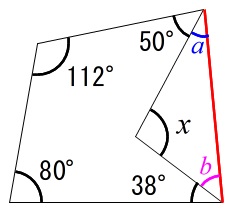
飯塚 弘貴 Hiroki Iizuka V Twitter 正解 7度 下図でa B C Dなので 印をつけた角の和は五角形と三角形の内角の和に等しい よって540 180 7度となる



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学




小学校5年 算数 正多角形の角の大きさ Youtube



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典




簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく
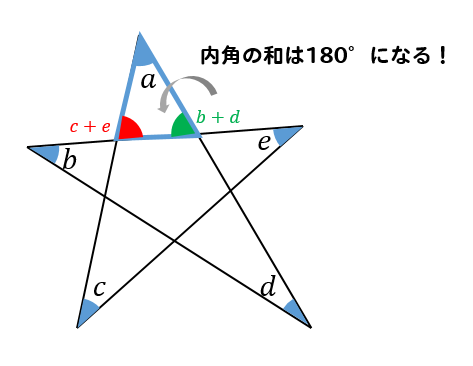



星形の角度 内角の和の求め方を問題解説 数スタ




この問題の答えはイなんですけど どうしてそうなるのかが分かりません Clear




多角形の内角の和 算数の公式覚えてますか



中学二年生の星形五角形の内角の和の求め方を教えてください 星 Yahoo 知恵袋



多角形の内角と外角 思考力を鍛える数学



2



数学得意な方お願いします 正五角形の1つの内角は何度になりますか その角度を求 Yahoo 知恵袋



5角形の内角の和



n角形 多角形 の内角の和の求め方



五角形の内角の和の求め方 久保塾 今治市の学習塾




中学2年生 覚えておくと便利な角度の関係 公式 個別進学教室マナラボ受験 教育情報サイト




数学 中2 51 多角形の内角と外角の和 基本編 Youtube



Http Www Mct Ne Jp Users Koavc Kon1 Data2 Es5 Ma 04 Pdf
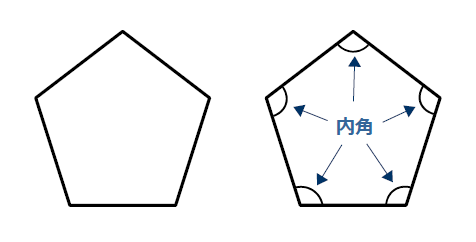



内角 ゆるゆるプログラミング




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
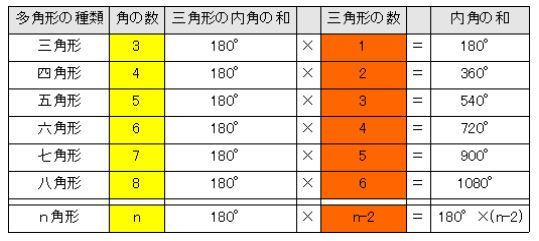



内角攻め それとも外角攻め すうがくラボのブログ




簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく




多角形の内角の和 は何度なのか を説明します おかわりドリル



南山中学女子部過去問題演習



3




十五角形 Wikipedia
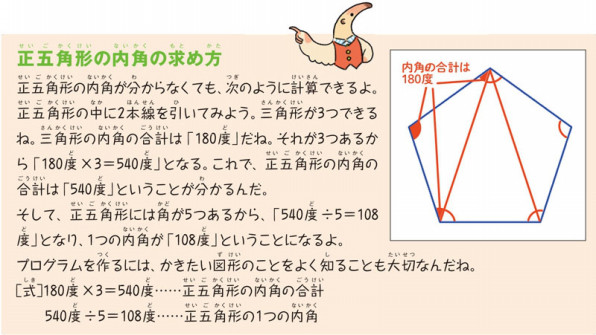



スクラッチ入門 16 正五角形をかいてみよう はじめる 楽しむ プログラミング こどもプログラミング教育のツボ ジャムハウス




スクラッチ入門 16 正五角形をかいてみよう はじめる 楽しむ プログラミング こどもプログラミング教育のツボ ジャムハウス



正五角形を描く ウソの国ー詩と宗教 戸田聡 St5402jp




中学2年の数学 動画 多角形の内角と外角の和 計算編の問題 19ch



この方法で星型五角形の五つの内角の和の求め方をおしえてください A Yahoo 知恵袋



五角形の内角の和について 五角形を三角形に分けて考えるとき 写真の中の上と下 Yahoo 知恵袋




無料 中2数学 発展問題 解答プリント 図形4 三角形の合同条件



Www Tsumugi Ne Jp Member Data Sm2 4 Sm2 4 3 Pdf




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学




正五角形に付随する角度と黄金比の関係 萌えとかプログラミングとか




多角形の内角の和 は何度なのか を説明します おかわりドリル



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス




五角形の内角の和 ワークシート スクールプレゼンター教材共有サイト スクプレ道場




中学数学 平行と合同 多角形と角 星形五角形の内角の和 Youtube



多角形の内角の和 勉強ナビゲーター




課題学習の指導 数学
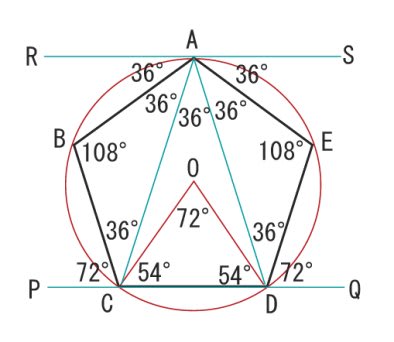



正五角形というだけで 分かる角度は 名寄 算数数学教室より




3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく



角度 五角形 中学から数学だいすき
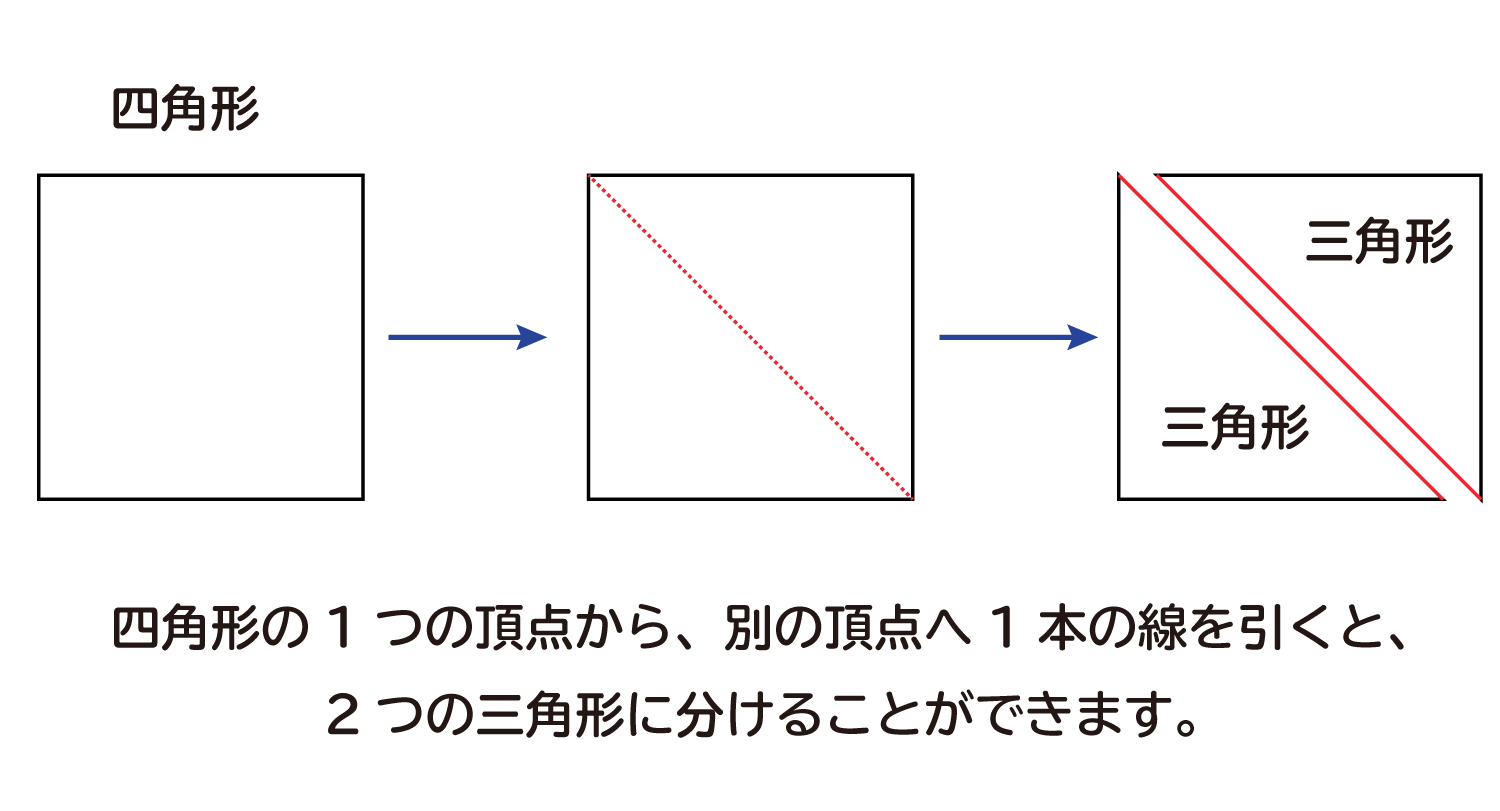



多角形の内角の和 は何度なのか を説明します おかわりドリル




正十五角形の1つの内角の大きさを求めなさい Clear
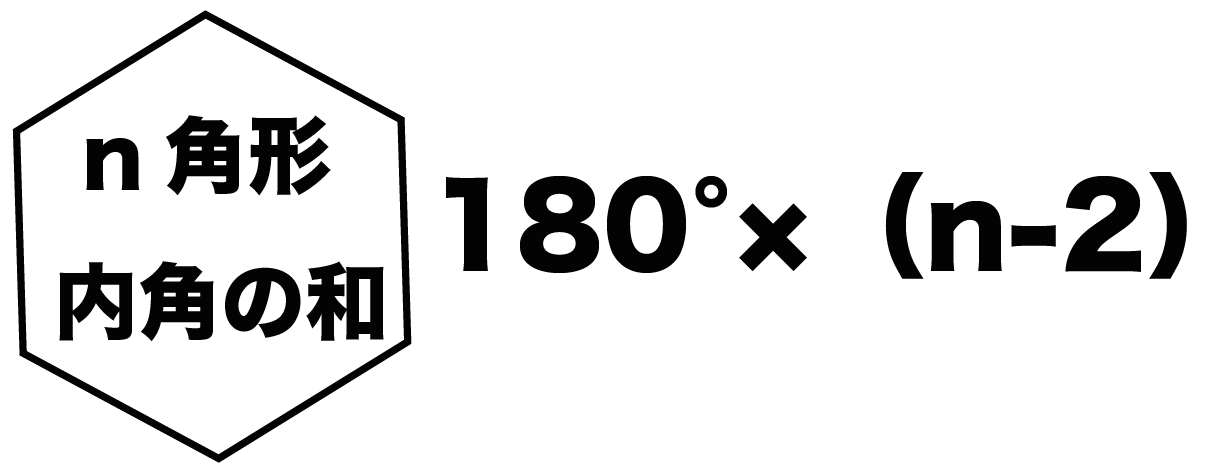



簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学




内角の和 180 N 2 外角の和 360 教遊者




多角形の性質 第2回 多角形の内角の和の求め方 算数パラダイス
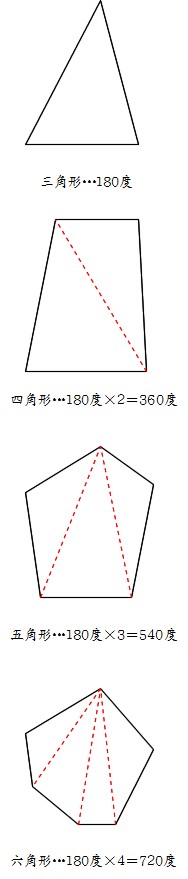



Math 多角形の内角の和 働きアリ
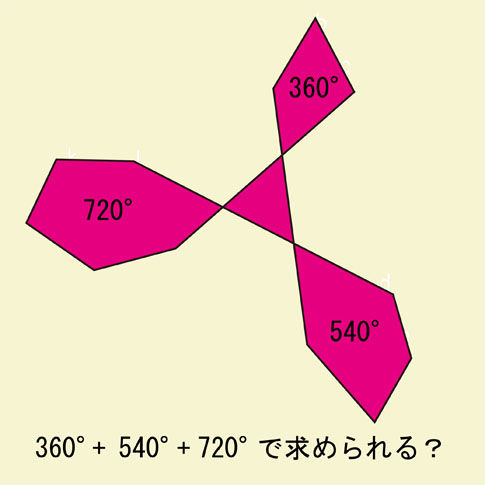



12個の角の和を求められますか 油断大敵を地で行く問題 秒刊sunday




内角の和の公式 内角の和が1800 の多角形は何角形 中学や高校の数学の計算問題
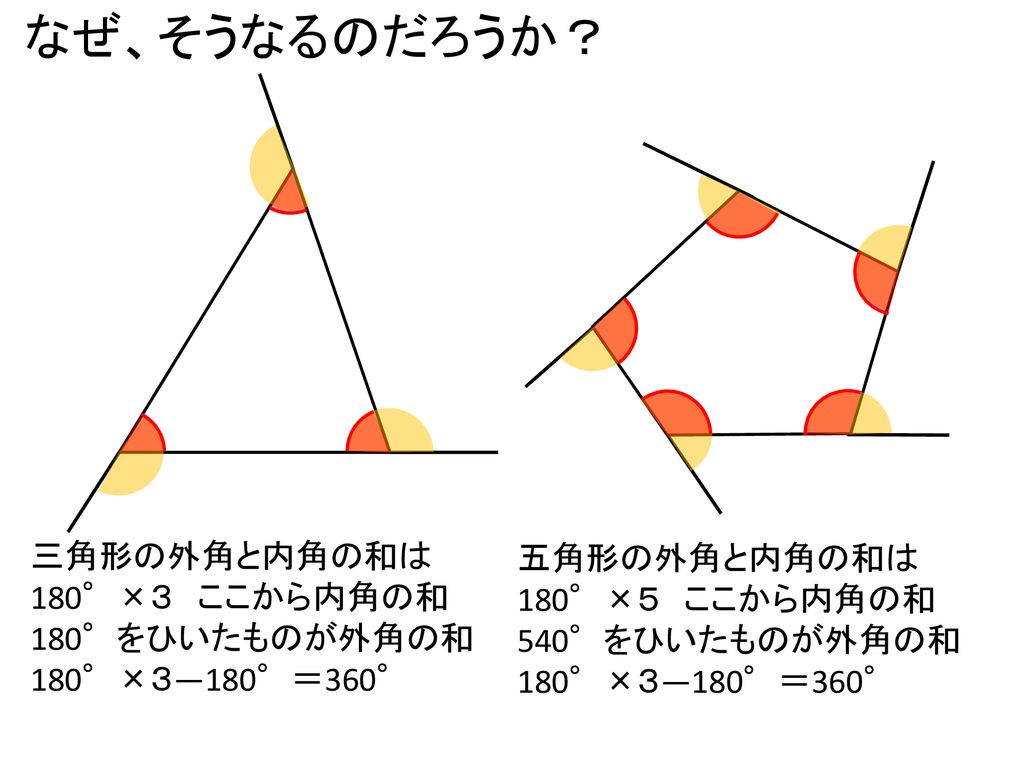



多角形の外角の和 凹型四角形の角 星形五角形の内角の和 Ppt Download



南山中学女子部過去問題演習




なぜ 求める角の大きさの和が星型の内部の五角形の内角の和に等しくなるのでしょうか Clear
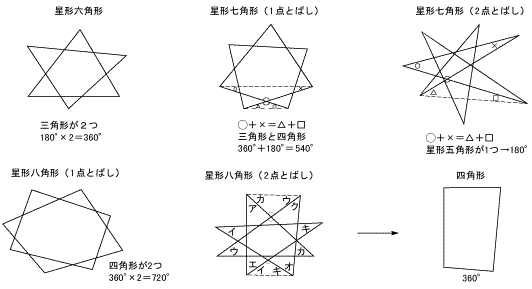



課題学習の指導 数学
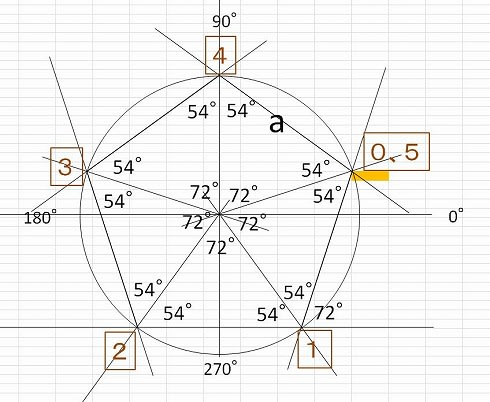



ペンタゴンボールの型紙 エクセルvbaで正五角形を作図してみましたpart 2 日だまりのエクセルと蝉しぐれ




8 Times31 Descubre Como Resolverlo En Qanda



0 件のコメント:
コメントを投稿