2次方程式の解の公式(虚数解含む) 3次方程式 フリ-ソフトwxMaximaによる高次,連立方程式の解き方 ===二次方程式の解き方=== (因数分解による方法) 解説 ≪原理≫ AB =0 ならば A =0 または B =0 ↑ 2つのものを掛けて0になるときは,どちらかが0だと 因数分解 式の計算 更新日時 四次式の因数分解(または方程式を解く)に関する問題は,以下の5パターンがあります。 パターン1A:普通に因数定理が使える場合 パターン1B:二次式×二次式に分解できる場合 パターン2:相反方程式 パターン31 次の式を因数分解しなさい。 (1)at-bt-ct (2)3ac-12a2 (3)24χ2-15χy12χz (1) t(a-b-c) (2) 3a(c-4a) (3) 3χ(8χ-5y4z)

三次项因式分解三次方分解因式方法
因数分解 3次
因数分解 3次-行列式 (3)数値計算 行列式 (4)基本性質による因数分解 == 行列式の基本性質を用いた因数分解 == このページでは,行列式の基本性質を使って,文字式の値を求める問題を扱う. 以下においては,これらの基本性質のうちで,主に次の2つを使って,文字式動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru




3次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ
因数分解を行う式を電卓に入力し「因数分解」ボタンを押してください。 置き換えや公式を連続して使うなどの複雑な因数分解では途中式も表示されますので解き方の手順がわかります。 この電卓は中学で習う因数分解に対応しています。 3次式などの高校レベルの因数分解には当電卓では対応していません。 やり直す場合は「クリア」ボタンを押すと電卓に入力1次式の因数分解は,共通因数でくくる変形があるだけですから,共通因数を考えます. (ab) x (ab) (a−b) = (ab) (xa−b) (答) この問題を a について整理しても間違いではありませんが,2次式の因数分解になるので次のようにやや複雑になります. a x 因数分解の工夫(3)(難)(4乗と複二次式・たすき掛け) 解説 中3数学 因数分解 標準問題 発展問題 前回までの内容でも、難関レベルの問題に対応できると思うが、
因数分解ができると、 二次以上の方程式を解く のに役立ちます。 因数分解の公式 ここでは、因数分解の \(2\) 乗の公式および \(3\) 乗の公式を確認していきます。 2 乗の公式 二次式を因数分解する公式は以下の通りです。これは、3次多項式を因数分解する方法に関する記事です。 彼は、グループ化による因数分解の方法と、自由用語の使用方法を探ります。 2の方法1:グループ化による因数分解 多項式を2つの部分にグループ化します。 多項式を2つの部分にグループ化すると、各セクションを個別に扱うことができます。 多項式x 3x6x18 = 0で作業しているとしましょう。 これを(x まずは「 3次方程式の解き方 」をまとめます。 11 3次方程式の解き方の流れ 3次方程式を解くには、基本的に因数分解をする必要があります。 2次以下の式に因数分解をして,それぞれの因数を解いていきます。
多項式の基本6|3次以上の展開と因数分解の公式の総まとめ 前々回の記事で説明したように,たとえば x 2 − 2 x − 2 = 0 のような簡単には因数分解できない2次方程式は,いったん解を求めることによって因数分解できるのでした. では,3次式では因数分解 中3 因数分解による2次方程式 中学生 数学のノート Clear 表紙 1 公開日時 21年07月23日 17時34分 更新日時 21年07月23日 17時44分 中学生 3年生 数学 2次方程式とその解き のように、 の2次の項、1次の項、定数項でできている式は、 公式1~3 を使って因数分解をします。 では、 和が、積が になる2つの数を見つけます。 なので、2つの数は と です。 公式1 で、 とすればよいのです。 例1 和が、積が → と 例2 和が、積が
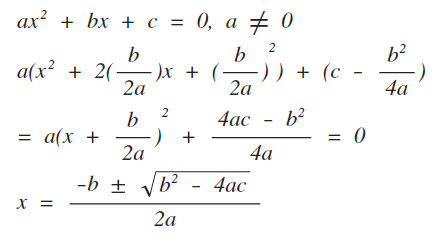



高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium



因式分解 A的3次方 B的三次方 C的三次方 3abc 腾讯视频
3次関数以上の因数分解 (1)因数分解の公式を当てはめる. (2)因数定理の利用する. F (α) = 0 → (x − α) が因数となる. 複数の文字を含む多項式の因数分解 (1)共通因数をくくり出す. (2)最低次数の文字を中心に整理する. (3)因数分解の公式を当てはめる数学Ⅰの式の計算で使う公式 指数法則 2次の乗数公式 3次の乗法公式 2次の因数分解 3次の因数分解 絶対値 a、bを実数とすると (※ただし、b≠0) 平方根 aを実数とすると a&g 3次式の因数分解では、展開の公式を逆に利用しよう。 3次式を因数分解するために、展開の公式を確実に覚えておこう。 係数の扱いに気をつけよう。 公式との対応関係を正しく読み取ろう。



因数分解公式の導出 3次式 受験数学って暗記 仮 高校受験 大学受験 楽天ブログ




如何因式分解三次多项式 12 步骤
因数定理を使って因数分解するには,与えられた整式を とおいて,適当な整数 に を代入して,ちょうど0になるものを探します. そういう意味では,人聞きがよくないですが,「因数分解は,ある程度はまぐれ当たりねらいです」.運が良ければ,速く当たり,運が悪ければ,なかなか当たり次の式を因数分解しなさい 2x 34x 248x 4x 2 y12xy9y3x 2 y 2 x 3 y10xy 3 12a 3 12a 2 3a 4a 316a 8x 318xy 2 pdfファイル3次式の因数分解 課題1 3次式は,基本的に因数定理を用いて因数分解しました。確認として,次の式を因数分解しましょう。 \(f(x) = x^3 x^2 6x 4\) 忘れてしまった方は「02 剰余の定理と因数定理」で確認(復習)しましょう。



三次方怎么因式分解 高三网



1 01的3次方分解 西瓜视频搜索
三次多项式一定能因式分解得出实数解,因为每个三次项都一定有个实根。三次方多项式如x 3 x 1含有无理实根,不能被因式分解成含有整数或有理数系数的多项式。虽然可以用立方方程因式分解,这种方程还是不能分解成一个"整数"多项式。 a n − b n a^nb^n a n − b n の因数分解公式を紹介しましたが, a n b n a^nb^n a n b n はどうなるでしょうか? 実は, n n n が奇数の場合には「 n n n 乗の差の因数分解公式」において, b b b を − bb − b と置き換えることで「 n n n 乗の和の公式」も作ることが step4 \((axb)(cxd)\)と因数分解する。 最後は簡単です。 たすきがけの図を見ればすぐに因数分解できます。 よって、\(2x^25x3\)を因数分解すると、 $$(x1)(2x3)$$ となります。 4 3次式の因数分解




因式分解




三次项因式分解三次方分解因式方法
数学B:100分100点満点 5題解答B1〜必答B1 小問集合 点 (1)(ア)4点 (2)(イ)4点 (3)(ウ)2点 (エ)2点 (4)(オ)2点 (5)(カ)2点 (キ)4点B21場合の数と確率(数学a3次式の因数分解 問題 \ ( (1)~~a^3b^3= (ab)^33ab (ab)を利用して, \\~~~~~~~a^3b^3c^33abc~~を因数分解せよ \\ (2)~~ (1)を利用して, (xy)^ 数学Ⅰ 数と式 因数分解(置き換えの利用) 式の計算はなるべく楽に、早く計算したいですよね。 入試でも必須の力です。 今回は、置き換えを利用した因数分解について解説します。 問 次の式を因数分解せよ (1) \ ( (x2y)5 (x2y)63次以上の因数分解 (例題→選択問題) ※ 3次以上の式の因数分解を行う強力な方法として「因数定理」があるが,これは数学iiで習う.数学iではもっと簡単に「因数分解公式」「置き換え」などで因数分解できるものだけを扱う.




因数分解 発展 三次式の因数分解 Youtube
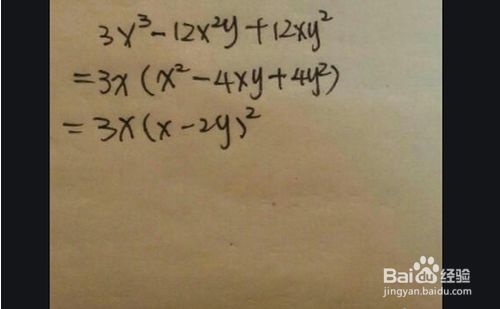



X的三次方怎么因式分解 百度经验
このページでは中3の数学で押さえておきたい 「多項式の計算」「因数分解」「平方根」「二次方程式」 の基礎ポイントをご紹介させていただきます。 こんなページも見られています! >>中学3年生の教科別学習ポイント 21年4月から中学校の教科書が因数分解の電卓 因数分解したい式を入力してください。 因数分解電卓 複雑な式を単純な因子の積に変換します。 この因数分解電卓は、任意の変数を含む多項式だけでなく、より複雑な関数を因数分解することができます。 数式の書式を表示 よってx³+3x²-2=(x+1)(x²+2xー2)と因数分解できます。 3.3次以上の高次方程式への応用 組み立て除法は3次式だけでなくそれ以上の次数の式でも用いることができます。 例えばx⁴+x³-7x²-x+6を因数分解してみましょう。



X3次方 Y3次方 怎么因式分解还有因式分解的思路 作业 慧海网




高校数学 因数分解 3乗が登場する因数分解の解き方をわかりやすく解説 数学の面白いこと 役に立つことをまとめたサイト
高校数学Ⅰで学習する因数分解の単元から 「3次式の因数分解のやり方」 について解説していきます。 3次式の因数分解の公式は次の通りです。一般的な3次式の因数分解は、因数定理を用いることで解くことができます。 まず、f(x)=x 3 x 2 x3とおきましょう。 そして、 f(p)=0となるpの値を見つけにいきます 。 具体的に、x=1とか、x=3といった値を代入して、調べていくわけですね。 21 3次式の因数分解 のときもやり方は同じです。 やり方がわかったら、実際に問題を解いてみましょう。 次の式を因数分解せよ。 3 まとめ 以上が、『展開・因数分解の公式一覧』です。 この単元の公式を、PDFファイルでプリント1枚にまとめました




3次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ
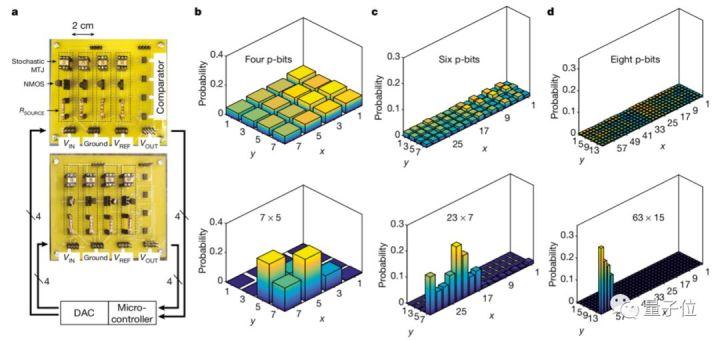



量子计算机遇到新对手 随机磁电路 因数分解更厉害 知乎



三次方因式分解技巧 西瓜视频搜索




一般三次方程式的解 配立方 Youtube



列竖式进行因式分解 知乎




如何因式分解三次多项式 12 步骤




分解因式方程的公式 三次方分解因式方法 三人行教育网 Www 3rxing Org




高1 三次式の展開と因数分解 高校生 数学のノート Clear




これらの公式がなかなか覚えられないです どのように覚えるのがよいのでしょうか Clear




高校数学 数 11 因数分解 3次式の公式編 Youtube




如何因式分解三次多项式 12 步骤




3次の因数分解の公式 数学が嫌いなんです




三次函數因式分解計算器factoring Cubic Function Calculator 學校沒有教的數學 學校沒有教的數學




3次方公式三次方分解因式重要公式 Kwame211的博客 Csdn博客 Azyvp



因式分解技巧pdf




3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す
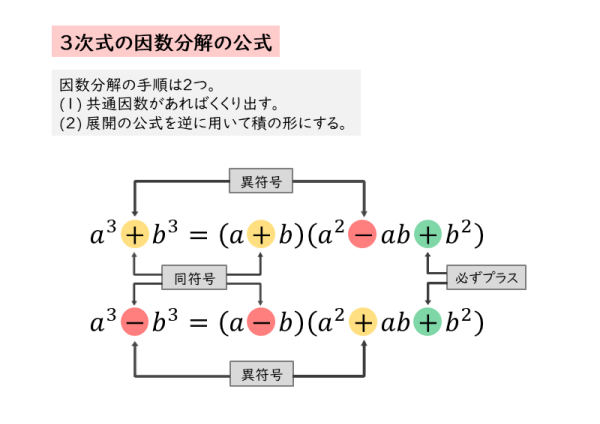



式と証明 3次式の因数分解について 日々是鍛錬 ひびこれたんれん




高校数学 因数分解公式と3次式の因数分解 A B C 3abc 受験の月




三次多项式因式分解三次多项式因式分解有什么方法吗




教學factorize Cubic Polynomial 因式分解三次多項式 Youtube
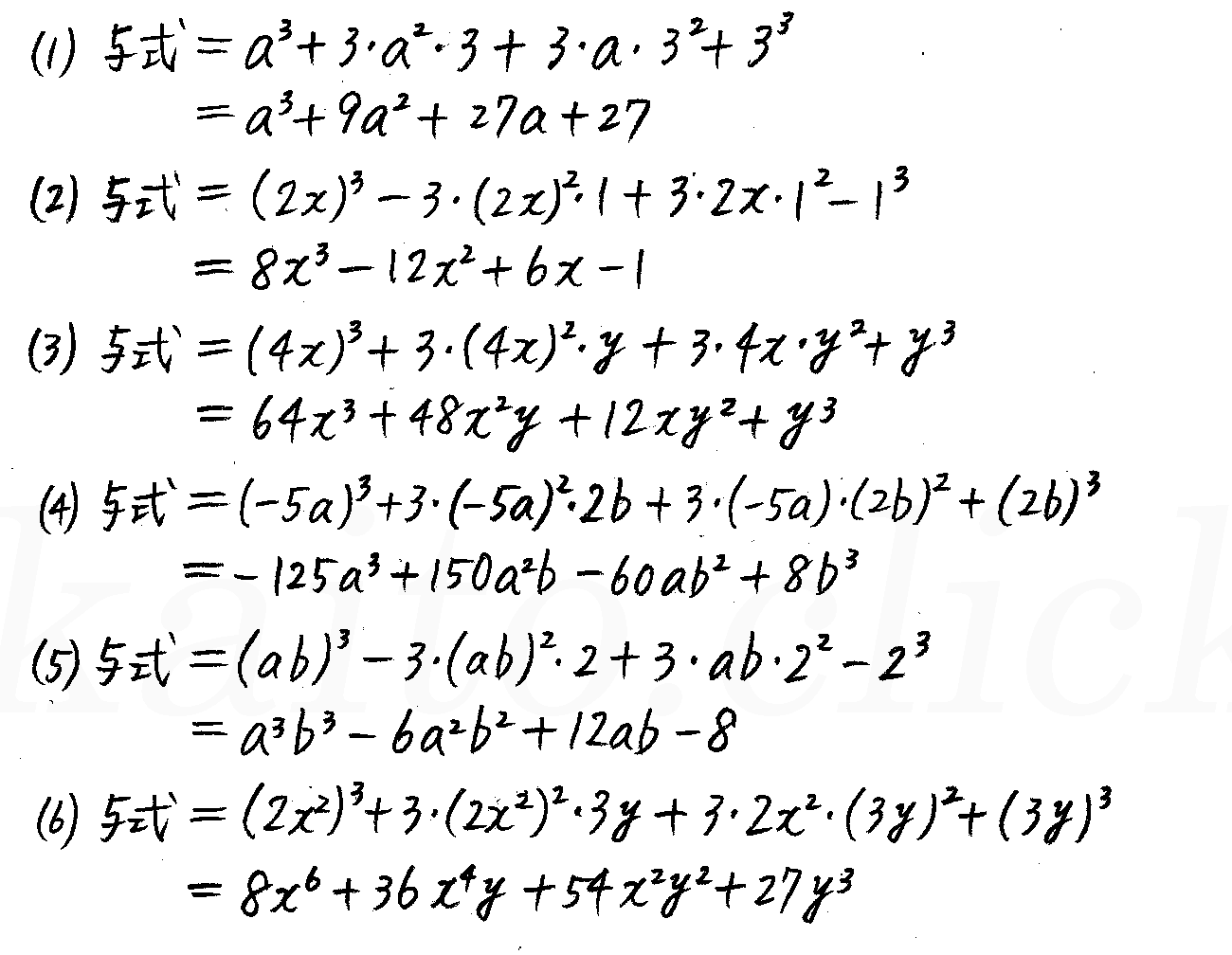



改訂版 4step数学 P6 1 3次式の展開と因数分解




如何因式分解三次多项式 12 步骤




如何因式分解三次多项式 12 步骤




赋值法因式分解 求对三次或高次多项式因式分解的方法 三人行教育网 Www 3rxing Org




X的三次方怎么因式分解 百度经验
(x-1).jpg)



Rgluijf8fecrpm




3次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ




3次式の因数分解の公式を徹底解説




因数分解その4 3次式 Youtube




高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium




X的三次方如何分解因式 搜狗搜索




複雑 な 因数 分解 展開の工夫と 2 難 順番の工夫 因数分解の利用 Amp Petmd Com



1 01的3次方分解 西瓜视频搜索




46 A3 Ab 3 3ab Ab A3b Descubre Como Resolverlo En Qanda




一元三次多项式因式分解的两种方法 Longlongqin的博客 程序员宅基地 一元三次因式分解步骤图 程序员宅基地



19 03 13因式分解法解一元三次方程 哔哩哔哩 つロ干杯 Bilibili




因数分解 8 交代式の因数分解 怜悧玲瓏 高校数学を天空から俯瞰する
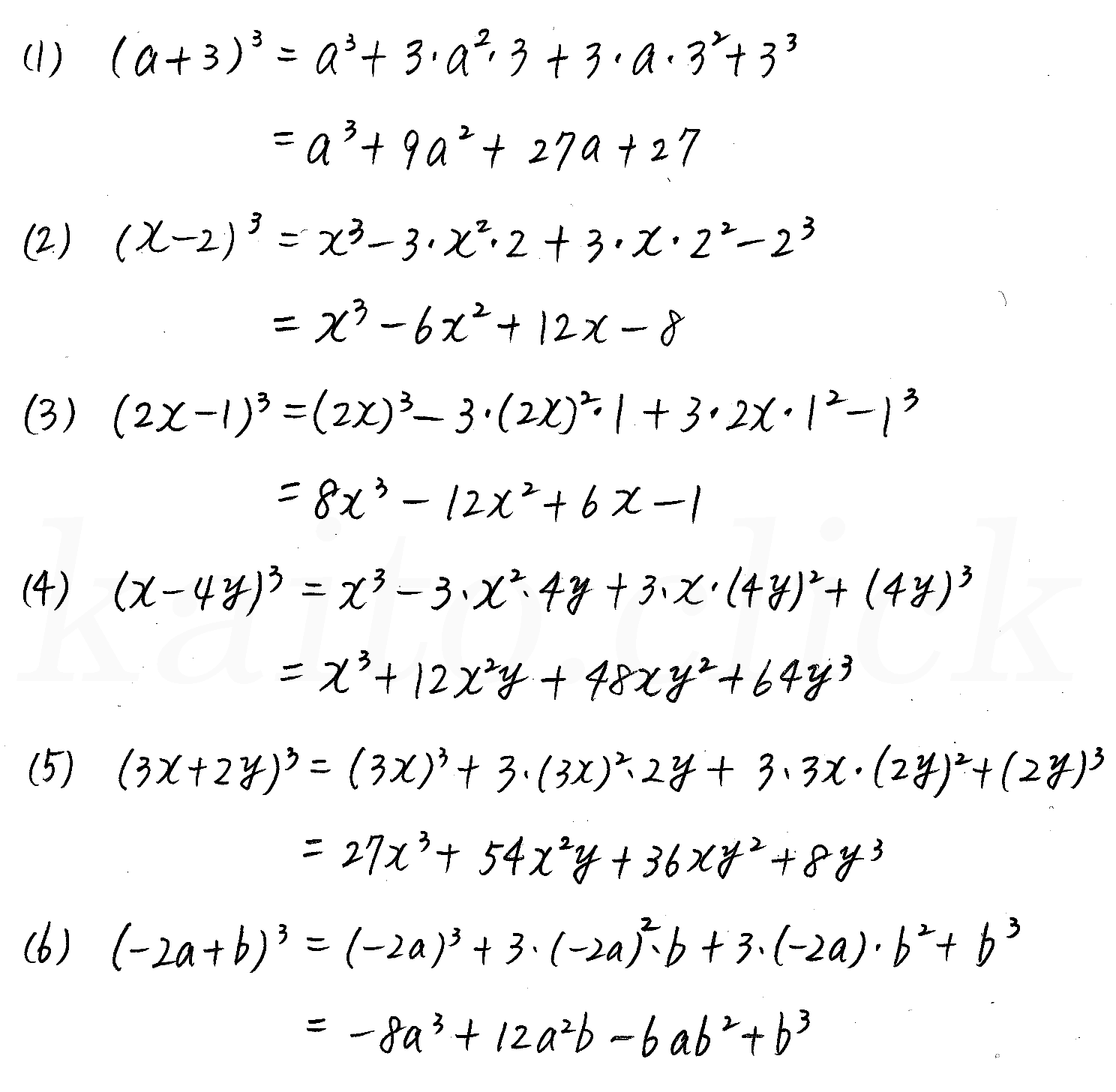



改訂版 3trial数学 P6 1 3次式の展開と因数分解




3次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ




三次项因式分解三次方分解因式方法
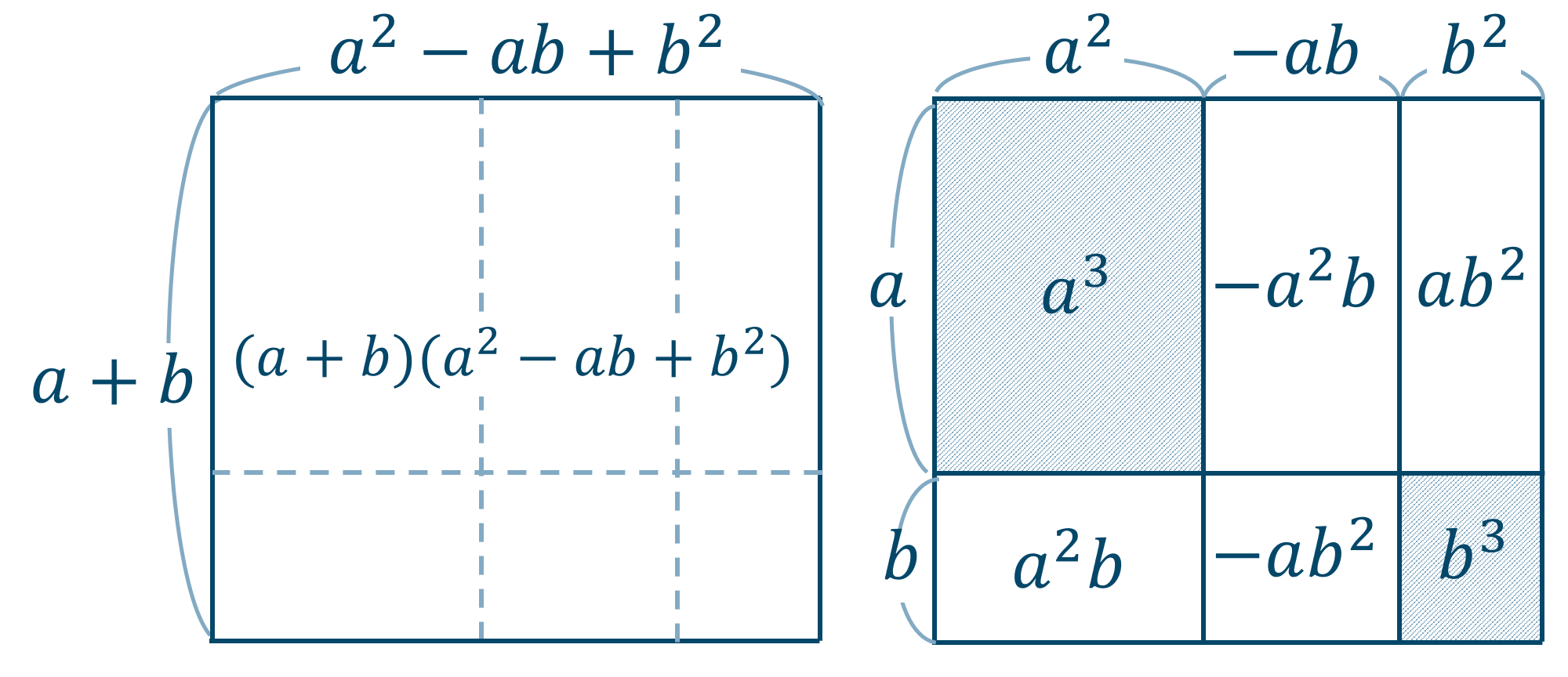



数学 3次式の因数分解の公式の使い方とコツ ページ 2 教科書より詳しい高校数学
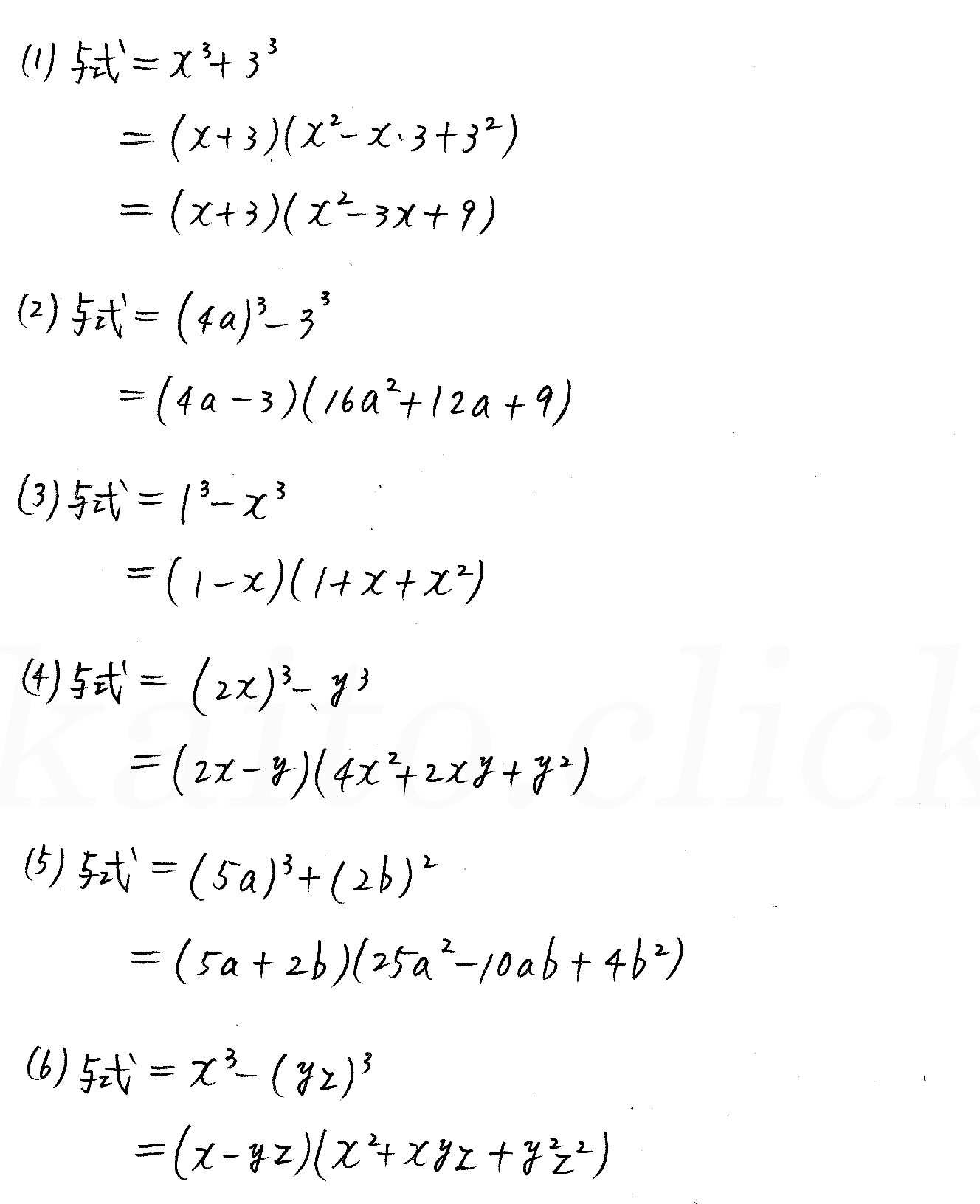



改訂版 4プロセス数学 P15 発展 3次式の因数分解




如何因式分解三次多项式 12 步骤




高校数学 3次式の展開 因数分解 公式 覚え方 計算方法 学校よりわかりやすいサイト




数学 B 3次式の因数分解 広島工業大 関西学院大 北海道医療大 東海大 大学入試数学の考え方と解法




A的3次方减b的三次方因式分解是多少 雨露学习互助



Http Mail Knu Edu Tw Syokou Calculus Ch1 4 Pdf



三次方公式
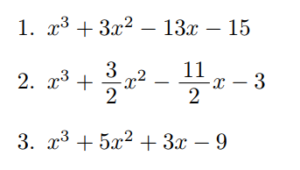



因数定理を利用した因数分解の練習問題 高校数学の知識庫




因式分解之待定係數法 一元三次多項式分解 每日頭條



三次方因式分解技巧 西瓜视频搜索




高校数学 因数定理と3次式の因数分解 練習編 映像授業のtry It トライイット



3次方的因式分解三次方的因式分解技巧和经典练习题




代数 因式分解并解一元三次方程式之三个相异有理数解 Youtube



三次関数の因数分解の仕方を教えてください 2x 3 3x 2 1 Yahoo 知恵袋




三次方 三次方程式展開




因式分解技巧 二元二次的分解 星空暗流 博客园




3次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ
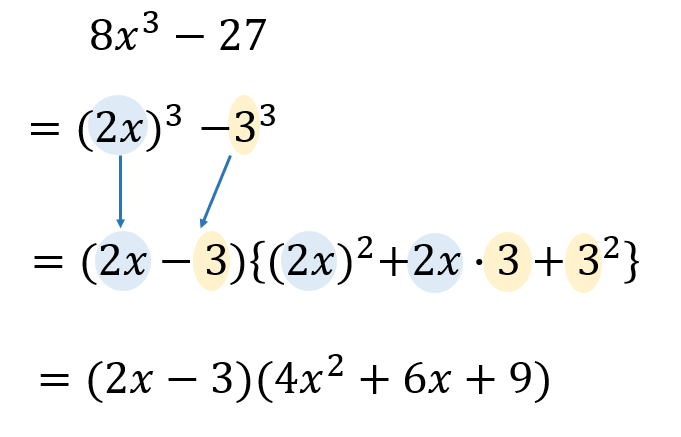



3次式の因数分解 公式とやり方について問題を使って解説 数スタ




3次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ



三次因式分解 3次方多项式有什么因式分解的方法举些例子 尚书坊



因数分解 6 3次の因数分解 怜悧玲瓏 高校数学を天空から俯瞰する



因式分解技巧pdf



Q Tbn And9gctgoae9bomuk0gymqhrkjzep3izucoijhp9evjmecua8k 13ra4 Usqp Cau




因数分解3 次 因数分解3次




设计一个一元多项式加法器 因式分解之待定系数法 一元三次多项式分解 哪怕是你的博客 Csdn博客




完了しました 因数分解3 次 ニスヌーピー壁紙



1




质因数分解 思维训练 Noip知识课堂




因数分解 怜悧玲瓏 高校数学を天空から俯瞰する




3次式の因数分解 公式とやり方について問題を使って解説 Youtube




完了しました 因数分解3 次 ニスヌーピー壁紙




高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium




文字が3つの因数分解 すうがくのいえ




3乗の因数分解 展開 公式 理系ラボ




3次式の因数分解 公式とやり方について問題を使って解説 数スタ



高次方程式 京極一樹の数学塾




1講 3次式の展開と因数分解 1節 式と計算 問題集 1章 式と証明




2 3b觀念01因式分解三次多項式 為什麼我們需要牛頓定理 Youtube




如何因式分解三次多项式 12 步骤



三次因式分解 3次方多项式有什么因式分解的方法举些例子 尚书坊




高校数学 因数分解公式と3次式の因数分解 受験の月




Aの6乗 64bの6乗の因数分解です 予習として1度解いたのですが Clear



Q Tbn And9gctgoae9bomuk0gymqhrkjzep3izucoijhp9evjmecua8k 13ra4 Usqp Cau



三次因式分解 3次方多项式有什么因式分解的方法举些例子 尚书坊




如何因式分解三次多项式 12 步骤




3次以上の展開と因数分解はどうなる 公式の総まとめ




X的三次方减8因式分解 X的三次方减8 X的三次方减8展开




第1章1講目 3次の因数分解 3次式の代表的な因数分解できますか ニコニコ動画




360影视 影视搜索




高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium



数と式の問題 京極一樹の数学塾



0 件のコメント:
コメントを投稿